O problema da construção de Quadrados Mágicos é conhecida desde a antiguidade. Trata-se de construir uma tabela quadrada e preenche-la com números naturais sequenciados, de modo que as somas de suas linhas, colunas e diagonais principais sejam constantes. Desse modo, um quadrado de ordem n, são inseridos os n2 primeiros números naturais, sendo a somas desses números:
A solução a ser encontrada em cada fileira, a Soma Mágica, será dada por:
É possível a construção de Quadrados Mágicos para qualquer n, exceto n = 2. Para n = 3 admite-se somente uma solução (desprezando inversões e rotações). Para n = 4 admite-se 880 possibilidades. E esse número cresce rapidamente nas ordens seguintes.
A ciência dos Quadrados Mágicos evoluiu de estudos nos séculos IX e X até a época de ouro do século XII, quando ela atingiu seu apogeu no Islã.
Abul Wafa Al-Buzjani (século X) desenvolveu dois métodos para construção de Quadrados Mágicos de ordem 5.
Primeiro método
Dispomos os n2 primeiros números naturais, para n = 5. Então a soma dos números 1+2+3+…+25 = 325 e a solução a ser encontrada será:
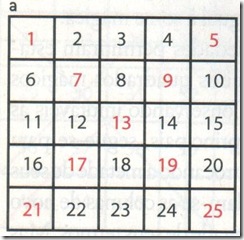
Mantemos os números das diagonais principais fixos, mostrados em vermelho na figura a:
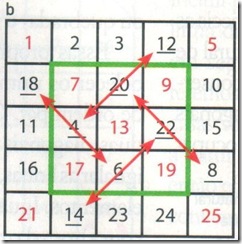
Trocamos os números do quadrado interior de ordem 3, contornado em verde, com os da casa distante de duas casas na diagonal, como mostra a figura b. As flechas em vermelho mostram os números a serem trocados:
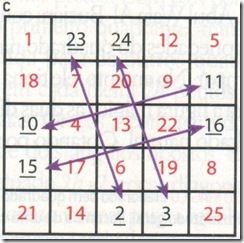
Trocamos, finalmente, os números das extremidades que ainda não foram trocados com aqueles da fileira oposta, conservando sua ordem de sucessão. As flechas em violeta mostram os números a serem trocados, como mostra a figura c:
Desse modo, a soma de cada linha, coluna e diagonais será igual a 65.
Segundo método:
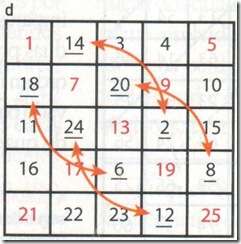
Dispomos os n2 primeiros números naturais, para n = 5. Mantemos os números das diagonais principais fixos, mostrados em vermelho na figura a:
Invertemos os pares de números aproximando a diagonal descendente. As setas em laranja mostram os números a serem trocados, como mostra a figura d:
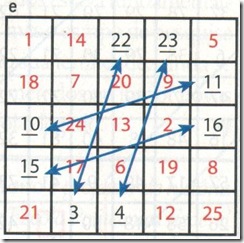
Trocamos os números restantes das bordas com as laterais opostas. As flechas em azul mostram os números a serem trocados, como mostra a figura e:
Desse modo, a soma de cada linha, coluna e diagonais será igual a 65. E o resultado obtido é diferente do encontrado na figura c pelo primeiro método.
Referências
[1] Scientific American – Ed. Especial nº 11 - Etnomatemática
Veja mais:
Quadrados Mágicos de Ordem Ímpar (Parte 1) no blog Matemágicas e Números
Quadrados Mágicos de Ordem Ímpar (Parte 2) no blog Matemágicas e Números
O Quadrado Mágico da Besta no blog Fatos Matemáticos

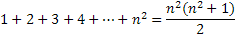



Muito bom
ResponderExcluirSou fã dos quadrados mágicos, tenho uma pequena pergunta para você.
Aonde posso encontrar resoluções de quadrados pares
6x6
8x8
etc
matemacere@yahoo.com.br
Olá Amigo,
ResponderExcluirEste método retirei de uma revista Scientific American Edição Especial nº11 Etnomatemática. Ainda tem mais sobre quadrados mágicos de ordem ímpar e de ordem par. Vou escanear as imagens e faço um novo post.
Achei uns links :
http://mathsforeurope.digibel.be/magic.htm
http://wba.novaloka.nl/magic-squares.html
PDF
http://www.math.binghamton.edu/zaslav/386.F09/delucchi.magic-squares.pdf
http://home.earthlink.net/~morgenstern/magic/make8.htm
http://www.win.tue.nl/~aeb/games/bf_magic.html
http://www.google.com.br/url?q=http://docs.google.com/gview%3Fa%3Dv%26q%3Dcache:lgfNC3QJMqYJ:www.tttpress.com/pdf/Ultimate-Magic-Square.pdf%2Bconstruction%2Bmagic%2Bsquare%26hl%3Dpt-BR%26gl%3Dbr%26pid%3Dbl%26srcid%3DADGEESjvu-bzquU97uI5rrvW3fxhp3x1FxjE3Kn0UQwF2fw-KI3bPzpLv8hTmW39CBzQ9E4m4ddaNrsEgdTMXdVZxcCt0O94TNp4Uj8VPQ1rNecDEz6V_-Ta7ztmqICT4Tv9c2eB4JOg%26sig%3DAFQjCNGDxBTTujLP0U85nKsUlfnYt6nBKA&ei=U3UES7H5JMqTnQfphOlr&sa=X&oi=gview&resnum=30&ct=other&ved=0CEkQxQEwCTgU&usg=AFQjCNGwW7Ln9Xm1MPooWt097xRmCmns-Q
Um abraço!
obrigado foi a cola de um trabalho
ResponderExcluir