Neste artigo veremos as demonstrações dos pontos notáveis de um triângulo: baricentro, incentro, circuncentro e ortocentro. Para uma melhor compreensão do que será estudado, vamos expor algumas definições iniciais:
1. Cevianas notáveis:
O nome ceviana foi dado a esses segmentos em homenagem ao matemático italiano Giovanni Ceva (1648-1734), que demonstrou teoremas importantes sobre elas. As cevianas aqui estudadas serão: mediana, bissetriz interna e altura.
1.1. Definição de ceviana:
Ceviana é todo seguimento que tem uma das extremidades num vértice qualquer de um triângulo e a outra num ponto qualquer da reta suporte ao lado oposto a esse vértice.
Reta suporte de um segmento, ou simplesmente suporte de um segmento, é a reta na qual esse segmento está contido.
onde $r$ é o suporte de $\overline{BC}$.
Conforme a definição, uma das extremidades da ceviana é um vértice. Podemos dizer que a ceviana é relativa a esse vértice, ou relativa ao lado oposto ao mesmo. A outra extremidade da ceviana é denominada pé. Assim, na figura acima, as cevianas $\overline{AA_1}$, $\overline{AA_2}$ e $\overline{AA_3}$ são relativas ao vértice $A$ ou também relativa ao lado $\overline{BC}$ e os pontos $A_1$, $A_2$ e $A_3$ são os pés dessas cevianas.
Cada vértice de um triângulo podem conter infinitas cevianas, estas podendo ser internas ou externas.
Dentre essas infinitas cevianas, há três que são muito importantes, por isso são chamadas de notáveis. São elas: mediana, bissetriz interna e altura. Veremos a seguir a cada uma delas.
1.1.1. Definição de mediana:
Mediana é toda ceviana que tem uma das extremidades no ponto médio de um lado.
Por convenção, os pontos médios dos lados opostos aos vértices $A$, $B$ e $C$ são denotados por $M_a$, $M_b$ e $M_c$, respectivamente e os comprimentos das medianas relativas aos mesmos são denotados por $m_a$, $m_b$ e $m_c$.
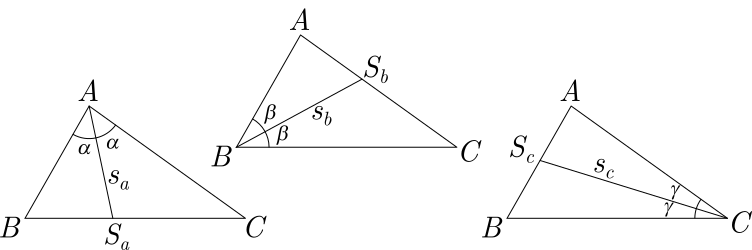
1.1.2. Definição de bissetriz interna:
Bissetriz Interna é toda ceviana que divide um ângulo interno em dois ângulos adjacentes e congruentes.
Por convenção, os pés das bissetrizes internas relativas aos vértices $A$, $B$ e $C$ são denotadas por $S_a$, $S_b$, e $S_c$, respectivamente, e os comprimentos das mesmas por $s_a$, $s_b$ e $s_c$.
1.1.3. Definição de Altura:
Altura é toda ceviana perpendicular a um lado ou ao seu suporte.
Por convenção, os pés das alturas relativas aos vértices $A$, $B$ e $C$ são denotados por $H_a$, $H_b$ e $H_c$, respectivamente, e os comprimentos dessas alturas por $h_a$, $h_b$ e $h_c$.
2. Pontos notáveis de um triângulo:
Para qualquer triângulo, valem as seguintes propriedades:
- P1) As três medianas concorrem num mesmo ponto;
- P2) As três bissetrizes internas concorrem num mesmo ponto;
- P3) As retas suportes das três alturas concorrem num mesmo ponto;
- P4) As mediatrizes dos lados concorrem num mesmo ponto.
Esses pontos de encontro das cevianas notáveis e das mediatrizes são denominadas pontos notáveis. São eles: baricentro, incentro, circuncentro e o ortocentro.
2.1. Baricentro (G):
As três medianas de um triângulo intersectam-se num mesmo ponto que divide cada mediana em duas partes, sendo que a parte que contém o vértice é o dobro da outra. Esse ponto é denominado baricentro do triângulo e é denotado por $\bf G$.
2.1.1. Demonstração do baricentro de um triângulo:
Seja o triângulo abaixo:
Por hipótese, temos que: $\overline{AM_a}$, $\overline{BM_b}$ e $\overline{CM_c}$ são medianas. Por tese, temos que:
$$\overline{AM_a}\ \cap \overline{BM_b} \ \cap \overline{CM_c}=G\\
\ \\
\overline{AG} = 2 \cdot \overline{GM_a}\\
\ \\
\overline{BG} = 2 \cdot \overline{GM_b}\\
\ \\
\overline{CG} = 2 \cdot \overline{GM_c}\\
$$
Seja $X$ o ponto onde $\overline{BM_b}\ \cap \overline{CM_c} = X$, que é o baricentro $G$ que queremos demonstrar. Se considerarmos os pontos médios $D$ e $E$ de $\overline{BX}$ e $\overline{CX}$, no triângulo $ABC$, teremos que:
Se:
$$\overline{AM_c} \equiv \overline{BM_c} \quad \text{e} \quad \overline{AM_b} \equiv \overline{CM_b}
$$
Então:
$$\overline{M_bM_c} \parallel \overline{BC} \quad \text{e} \quad \overline{M_bM_c} = \frac{\overline{BC}}{2}
$$
E se:
$$\overline{XD} \equiv \overline{BD} \quad \text{e} \quad \overline{XE} \equiv \overline{CE}
$$
Então:
$$\overline{DE} \parallel \overline{BC} \quad \text{e} \quad \overline{DE}=\frac{\overline{BC}}{2}
$$
Resultando em:
$$\overline{M_bM_c} \parallel \overline{DE} \quad \text{e} \quad \overline{M_bM_c} \equiv \overline{DE}
$$
Logo, $M_bM_cDE$ é paralelogramo. Então:
$$\overline{DX} \equiv \overline{XM_b} \Longrightarrow \overline{CX} = 2 \cdot \overline{XM_c} \tag{1}
$$
e
$$\overline{EX} \equiv \overline{XM_c} \Longrightarrow \overline{BX} = 2 \cdot \overline{XM_b} \tag{2}
$$
Logo, a mediana $\overline{BM_b}$ intersecta a mediana $\overline{CM_c}$ no ponto $X$, tal que:
$$\overline{CX} = 2 \cdot \overline{XM_c}
$$
Tomando-se as medianas $\overline{AM_a}$ e $\overline{CM_c}$ e sendo $Y$ o ponto tal que:
$$\overline{AM_a} \cap \overline{CM_c} = Y
$$
De modo análogo, concluímos que:
$$\overline{CY} = 2 \cdot \overline{YM_c} \tag{3}
$$
e
$$\overline{AY} = 2 \cdot \overline{YM_a} \tag{4}
$$
De $(1)$ e $(2)$ vem que $X=Y$. Se chamarmos esse ponto $X=Y$ de $G$ e considerarmos $(1)$, $(2)$ e $(4)$, temos que:
$$\overline{AM_a} \cap \overline{BM_b} \cap \overline{CM_c} = G
$$
E assim:
\begin{cases}\overline{AG} = 2\cdot \overline{GM_a}\\
\ \\
\overline{BG} = 2 \cdot \overline{GM_b}\\
\ \\
\overline{CG} = 2 \cdot \overline{GM_c}
\end{cases}
$\longrightarrow$ Leia o artigo sobre As coordenadas do baricentro de um triângulo
2.2. Incentro (I):
As três bissetrizes internas de um triângulo intersectam-se em um mesmo ponto. Esse ponto é chamado de incentro e é denotado por $\bf I$ e se encontra à igual distância dos lados do triângulo.
- O incentro é o centro da circunferência inscrita no triângulo.
2.2.1. Demonstração do incentro de um triângulo:
Seja o triângulo abaixo:
Por hipótese, temos que $\overline{AS_a}$, $\overline{BS_b}$ e $\overline{CS_c}$ são bissetrizes internas. Por tese, temos que:
$$\overline{AS_a} \cap \overline{BS_b} \cap \overline{CS_c} = I\\
\ \\
\text{e}\\
\ \\
\text{d}_{I,S_a} = \text{d}_{I,S_b} = \text{d}_{I, S_c}
$$
Seja o ponto $I$ o ponto onde:
$$\overline{BS_b} \cap \overline{CS_c} = I
$$
Que é o incentro que queremos demonstrar. Se:
$$I \in \overline{BS_b} \Longrightarrow \text{d}_{I,S_a}=\text{d}_{I,S_c}\\
\ \\
\text{e}\\
\ \\
I \in \overline{CS_c} \Longrightarrow \text{d}_{I,S_a}=\text{d}_{I,S_b}
$$
Então:
$$\text{d}_{I,S_b} = \text{d}_{I, S_c}\\
\ \\
I \in \overline{AS_a}
$$
Logo:
$$\overline{AS_a} \cap \overline{BS_b} \cap \overline{CS_c} = I\\
\ \\
\text{e}\\
\ \\
\text{d}_{I,S_a} = \text{d}_{I,S_b} = \text{d}_{I, S_c}
$$
$\longrightarrow$ Leia o artigo Teorema da bissetriz interna
2.3. Circuncentro (O):
As mediatrizes dos lados de um triângulo intersectam-se em um mesmo ponto. Esse ponto é chamado de circuncentro e é denotado por $\bf O$, podendo ser interno, externo ou coincidente.
- O circuncentro é o centro da circunferência circunscrita a um triângulo.
Circuncentro interno: se o triângulo for acutângulo:
Circuncentro externo: se o triângulo for obtusângulo:
Circuncentro coincidente: se o triângulo for retângulo:
2.3.1. Demonstração do circuncentro de um triângulo:
Seja o triângulo:
Por hipóteses, temos que $m_a$, $m_b$ e $m_c$ são mediatrizes de $\overline{BC}$, $\overline{AC}$ e $\overline{AB}$, respectivamente. Por tese, temos que:
$$m_a \cap m_b \cap m_c =O\\
\ \\
\text{e}\\
\ \\
\overline{OA} \equiv \overline{OB} \equiv \overline{OC}
$$
Seja $O$ o ponto onde:
$$m_b \cap m_c = O
$$
Que é o circuncentro que queremos demonstrar. Se:
$$O \in m_b \Longrightarrow \overline{OA} \equiv \overline{OC}\\
\ \\
\text{e}\\
\ \\
O \in m_c \Longrightarrow \overline{OA} \equiv \overline{OD}
$$
Então:
$$\overline{OB} \equiv \overline{OC}\\
\ \\
\text{e}\\
\ \\
O \in m_a
$$
Logo:
$$m_a \cap m_b \cap m_c = O\\
\ \\
\text{e}\\
\ \\
\overline{OA} \equiv \overline{OB} \equiv \overline{OC}
$$
2.4. Ortocentro (H):
As três retas suportes das alturas de um triângulo intersectam-se em um mesmo ponto. Esse ponto é chamado de ortocentro e é denotado por $\bf H$, podendo ser interno, externo ou coincidente.
Ortocentro interno: se o triângulo for acutângulo:
Ortocentro externo: se o triângulo for obtusângulo:
Ortocentro coincidente: se o triângulo for retângulo:
2.4.1. Demonstração do ortocentro de um triângulo:
Seja o triângulo:
Por hipótese, temos que $\overleftrightarrow{AH_a}$, $\overleftrightarrow{BH_b}$ e $\overleftrightarrow{CH_c}$ são retas que contêm as alturas. Por tese, temos que:
$$\overleftrightarrow{AH_a} \cap \overleftrightarrow{BH_b} \cap \overleftrightarrow{CH_c} = H
$$
Que é o ortocentro que queremos demonstrar.
Pelos vértices $A$, $B$ e $C$, traçamos retas paralelas aos lados opostos obtendo o triângulo $MNP$. Temos que:
\begin{cases}A \in \overline{NP} \quad \text{e} \quad \overline{NP} \parallel \overline{BC}\\
\ \\
B \in \overline{MP} \quad \text{e} \quad \overline{MP} \parallel \overline{AC}\\
\ \\
C \in \overline{MN} \quad \text{e} \quad \overline{MN} \parallel \overline{AB}
\end{cases}
Analisando o triângulo, temos que:
- $APBC$ é paralelogramo se $\overline{AP} \equiv \overline{BC}$
- $ABCN$ é paralelogramo se $\overline{AN} \equiv \overline{BC}$
Então:
$$A \text{ é o ponto médio de }\overline{NP} \tag{5}
$$
Em contrapartida $\overleftrightarrow{AH} \perp \overline{BC}$, então:
$$\overline{NP} \parallel \overline{BC} \Longrightarrow \overleftrightarrow{AH_a} \perp \overline{NP} \tag{6}
$$
De $(5)$ e $(6)$ temos que a reta $\overleftrightarrow{AH_a}$ é a mediatriz de $\overline{NP}$.
Analogamente, obtemos que $\overleftrightarrow{BH_b}$ é a mediatriz de $\overline{MP}$ e $\overleftrightarrow{CH_c}$ é a mediatriz de $\overline{MN}$.
Logo, considerando o triângulo $MNP$, as mediatrizes intersecta-se em um mesmo ponto $H$:
$$\overleftrightarrow{AH_a} \cap \overleftrightarrow{BH_b} \cap \overleftrightarrow{CH_c} = H
$$
$\longrightarrow$ Leia o artigo Construção geométrica de perpendiculares
Referências:
- Fundamentos de Matemática Elementar, V9 - Geometria Plana, Osvaldo Dolce, Ed. Atual
- Elementos de Geometria e Desenho Geométrico, V1, José Carlos Putnoki, Ed. Scipione
Links para este artigo:
Veja mais:
- Teorema da base média de um triângulo
- Teorema do ângulo inscrito
- Os pontos notáveis de um triângulo utilizando o Geogebra no blog do Professor Edigley
Histórico de revisão:
- Revisão em 10/10/2021: atualização das imagens e inserção de fórmulas em $\LaTeX$
Software utilizado:
- Inkscape


















Olá,
ResponderExcluirParabéns !!! Seu blog ganhou um selo. Visite o meu blog para saber como proceder para inserir o seu selo. Siga as regras.
Abraços,
http://www.mfmatematica.blogspot.com
ótimo; parabéns!
ExcluirMuito legal! Explicações perfeitas! Foi muito útil.(Imagens muito boas!)
ResponderExcluirsiim siim so faltou conclusao pra ficar perfeito
ExcluirObrigado! Procuro colocar imagens em tamanho grande, pois assim quem copiar poderá editá-la melhor.
ResponderExcluirAbraços.
Ola,
ResponderExcluirGostei também deste post que explica detalhadamente os pontos notáveis em um triângulo. Recentemente escrevi sobre a mediana e irei fazer um comentário no final do post.
Abraços!!
Legal Prof. Paulo. Preciso reestruturar este post para redimensionar as imagens, pois ficaram grandes demais neste novo template e aproveito e incluo o link de sua postagem.
ResponderExcluirUm abraço!
Realmente muito bom. Parabéns!
ResponderExcluirobrigada ajudou no meu trabalho!
ResponderExcluirJá foi útil!!!!!
Xau
Maravilha!! Que bom que te ajudou! Obrigado pela visita!
ResponderExcluirAbraços!
Parabens seu blog Ajudou MUITO!!!!
ResponderExcluirMeu trabalho vai ser nota 10
Valeeuu pelo blog =]
Obrigado. Volte sempre!
ResponderExcluirÓtimas demonstrações!! Me ajudou muiiiiito!! Vlw
ResponderExcluirObrigado e volte sempre!!
ResponderExcluirValeu amigo, bem completo este artigo!
ResponderExcluirAbçs
Zé
valeu msm me ajudo muito na prova
ResponderExcluirASS:vitor grassi
Maravilha!
ResponderExcluirmuito bom, gostei também das imagens, ficaram muito boas. Silas
ResponderExcluirnão tem o que eu kero
ResponderExcluirsinto muuito!!
Não sinta, amigo. Seria impossível eu colocar aqui um conteúdo que sirva para todos.
ResponderExcluirObrigado e um abraço.
Vlw cara.
ResponderExcluirTava precisando mto disso em minha prova.
booooooooooooooom ,obg
ResponderExcluirMuito bom, muito bom mesmo! Adorei!
ResponderExcluirEu que agradeço!
ResponderExcluir$muito bom meu ajudou muito mesmo vlw e abraços$
ResponderExcluirMuito bom
ResponderExcluirInteressante!Hoje fiz prova de OFA (professor do estado) e por íncrivel que pareça(coincidência??)
ResponderExcluirencontrei vários tópicos neste blog que são semelhantes às questões da prova.Pena que vi hoje depois da prova.
Espero que tenha se saído bem.
ResponderExcluirObrigado pela visita e comentário.
Volte sempre.
Um abraço.
Muito boas as demonstrações... Como você consegue fazer uma coisa tão bem feita sem ganhar nada (monetariamente)? Rsrsrsrsrs...
ResponderExcluirSeu blog é perfeito uma verdadeira biblioteca matemática...
A propósito, bonitinha sua filha... :)
Pois é amigo, puro prazer! Enquanto o Ministério da Cultura concede verba de 1,3 milhões para criar um blog da senhora Bethânia, os blogs educativos sobrevivem pelo simples prazer de copartilhar o conhecimento. Quem sabe daqui há alguns anos (219, 327 anos?) não ganharemos algum incentivo financeiro para continuarmos.
ResponderExcluirUm abraço e obrigado pela visita!
Professor é o que se vê num país onde a vaidade e o perfunctório prevalecem sobre o que realmente importa, que é a educação de um povo, que tem muito o que aprender, de começo a cumprir suas obrigações e exigir seus direitos
Excluirnossa...vlw msm,tava presisando disso...
ResponderExcluirCaro Kleber... hoje não vou elogiar (Muita gente já faz isso).Vc contribui muito para o ensino e divulgação da Matemática e o blog é ótimo[ponto!]
ResponderExcluirVou pedir para dar uma "arrumadinha" em
"Se-gui-mento" e no termo "interceptar" cujo termo mais adequado é intersectar pois interceptar está para interromper e não é o caso.
Nada além disso.
Sucesso a vc
Vocês sabeeem das cooisas estão de parabéns ;D'
ResponderExcluirObrigado Pamela. Bons estudos. Volte sempre!
ResponderExcluirÓtimas informações, me ajudaram num trabalho de geometria, obrigada !
ResponderExcluirpodia dar uma melhorada na definição
ResponderExcluirAmigo, não vejo em que melhorar as definições. Se tiver uma ideia, me avise.
Excluirola,faço 8 ano o meu nome e evelinni valeu a pena seu blog , pois me ajudou muito.
ResponderExcluirAdorei este blog, agora tirei todas as minhas dúvidas! Muito bom, me ajudou bastante...
ResponderExcluirCaro professor Kleber gostaria que o senhor abordasse um assunto que muito me interessa, e creio que a muitos outros colegas,"Transformadas de Laplace" e "Análise de Fourier", principalmente focando o aspecto prático das aplicações que pode fazer desses recursos da matemática.
ResponderExcluirAtenciosamente.
Eng. Civil Jurandyr de Araujo Junior.
Olá Jurandyr, como vai?
ResponderExcluirRealmente não tenho nenhum artigo sobre os temas sugeridos. Tenho um ivro da coleção Schaum sobre as transformadas de Laplace. Vou ver se faço alguma coisa. De qualquer forma, sugiro que procuro no blog do Prof. Paulo:
http://fatosmatematicos.blogspot.com.br/
Um abraço.
muito bom
ResponderExcluirAh, muito bom !
ResponderExcluirFiquei até excitado ao ver esta página !
Professor Kleber, estou com um problema sobre ortocentro e não consigo resolver de forma alguma, vou tentar passar para texto a figura do triangulo: Um triangulo ABC, onde ABC=3α, HAC=α, HCA=20°, H é o ortocentro. Qual o valor de α. Desde já agradeço a sua atenção. Charles Moreira
ResponderExcluirCharles, considere o triângulo $ABC$. O ortocentro é o ponto $H$, que é o ponto de encontro das alturas. Considere os pontos $A'$, $B'$ e $C'$ que são os pontos de encontro das alturas referentes aos ângulos $A$, $B$ e $C$, respectivamente.
ResponderExcluirConsiderando os dados que o problema fornece, do triângulo $CAH$, $ \hat{A}= \alpha$ e do triângulo $HCA$, $ \hat{C}=20$. Assim, do triângulo $CAA'$, $ \hat{C}=20+ \beta$. Então temos que:
$$180= 90+ \alpha + (20+ \beta) \qquad(1)$$
E do triângulo $ABC$ temos que:
$$180=( \alpha + \beta)+3 \alpha +(20+ \beta) \qquad(2)$$
Igualando $(1)$ com $(2)$, obtemos:
$$ ( \alpha + \beta)+3 \alpha +(20+ \beta)=90+ \alpha + (20+ \beta)$$
$$90=3\alpha +\beta \qquad(3)$$
Do triângulo $ACC'$, temos que:
$$180=(\alpha +\beta)+90+20$$
$$\alpha=70-\beta \qquad(4)$$
Substituindo $(4)$ em $(3)$, obtemos:
$$90=3(70-\beta)+\beta$$
$$\beta=60$$
Substituindo $\beta$, obtemos $\alpha=10$
Espero ter sido claro. Qualquer dúvida deixe um comentário.
Abraços!
parabéns!
ResponderExcluirParabéns, professor!
ResponderExcluirEstou fazendo Eng. Elétrica e suas postagens têm me ajudado bastante em Desenho Técnico I.
Olá amigo. Obrigado pela visita e se dispor a comentar. Sinto-me realmente recompensado. Acredito que as aulas de desenho geométrico deveriam ocorrer ainda no ensino fundamental. Ficou uma lacuna que existe no ensino público brasileiro.
ExcluirUm abraço.
Olá, Kleber!
ResponderExcluirMais uma vez cá estou eu em uma de suas publicações apreciando suas ótimas explicações... Me ajudou muito com esse conteúdo só que fiquei meio confuso com relação a diferença entre circuncentro e ortocentro que a meu ver parece a mesma coisa, já que ambos envolvem as mediatrizes, ou será que entendi errado? Poderia me explicar melhor isso Kleber... Desde já agradeço a atenção...
Att. Romirys Cavalcante
Olá Romirys,
ExcluirAcredito que se confundiu, pois para o circuncentro usa-se as mediatrizes; já para o ortocentro, usa-se as alturas.
Para encontrarmos o circuncentro de um triângulo, utilizamos as mediatrizes de seus lados. A intersecção dessas mediatrizes é o ponto $O$, que é o centro da circunferência circunscrita ao triângulo.
Para encontrarmos o ortocentro de um triângulo, utilizamos as alturas. A intersecção das alturas é o ponto $H$.
Espero ter esclarecido.
Abraços!
Olá. Parabéns pela postagem! Antes de ver seu blog eu achava que todos esses pontos eram iguais! rsrsrs Agora vi que não são! Muito obrigado!
ResponderExcluirNão entendi a parte da demonstração do baricentro onde começam a entrar numerais, como M1, M2 e M3... Procurei, mas eles não constam na imagem.
ResponderExcluirRealmente houve uma confusão nos índices, sendo ora indicados como $a, b, c$, ora $1,2,3$. Considere que os índices: $a = 1$, $b = 2$ e $c = 3$. Com isso pode-se acompanhar o restante da demonstração.
ExcluirObrigado pela observação. Abraços.
no texto não ficou definido o conceito de mediatriz
ResponderExcluirÉ verdade. Pelo fato de ser usada em várias partes do texto. Assim que puder farei a inclusão.
ExcluirUm abraço!
no geral achei muito bom
ResponderExcluirFico feliz em ter encontrado essa postagem. Não conhecia o blog, mas gostei bastante da explicação baseada totalmente nos conceitos. É raro encontrar textos assim porque a maioria dos autores consideram que o aluno que está lendo não sabe nada do assunto, então eles tentam simplificar ao máximo possível e, nessa simplificação, alguns acabam deixando de lado o conteúdo. Não foi o que aconteceu aqui. Nesse caso, o autor considera que a pessoa que está lendo já tem uma certa noção do que seja bissetriz interna, mediana, altura e mediatriz e apenas atua no sentido de revisar os conhecimentos já adquiridos previamente. Muito obrigado, foi uma leitura prazerosa.
ResponderExcluirMuito boa a página. Explicações diretas e de fácil compreensão. Parabéns!!!
ResponderExcluirMuito Obrigado!! Estava precisando falar sobre as propriedades de um triângulo na minha pesquisa!!! vlw msm !!
ResponderExcluirvaleu apena vai me ajudar muito
ResponderExcluirNa demonstração das medianas, quem é AM3, BM3, AM2, CM2, M2 E M3?
ResponderExcluirameeeiiiiii, ajudou eu e minhas amigas Natalia, Izabel e Nayara a fazer o trabalho da professora Manú
ResponderExcluir