Integração por Substituição Trigonométrica

Há meios diferentes para integrar uma função e para cada integral, devemos identificar qual o melhor dos métodos a aplicar. Somente resolvendo diversos exemplos para podermos nos familiarizar com cada um desses métodos.

A substituição trigonométrica é uma técnica de integração muito utilizada quando ocorre integrandos algébricos. Ela se baseia no fato que identidades trigonométricas muitas vezes possibilitam a substituição de um função algébrica por uma função trigonométrica, que pode ser mais facilmente integrada.

No caso de integração por substituição trigonométrica, um integrante que contenha uma das formas:

$$\begin{gather*} \sqrt{a^2-x^2} \tag{I} \\ \ \\ \sqrt{a^2+x^2}\tag{II}\\ \ \\ \sqrt{x^2-a^2}\tag{III} \end{gather*}$$

sendo $a$ uma constante positiva e não tendo nenhum outro fator irracional, pode ser transformado numa integral trigonométrica mais familiar, utilizando substituições trigonométricas ou com o emprego de uma nova variável.

Para os três casos acima, utilizamos as identidades trigonométricas:

$$\begin{gather*} 1-\text{sen}^2(\theta) = \cos^2(\theta) \tag{1}\\ \ \\ 1+\text{tg}^2(\theta) = \text{sen}^2(\theta)\tag{2}\\ \ \\ \text{sec}^2(\theta)-1 = \text{tg}^2(\theta)\tag{3} \end{gather*}$$
Vamos ver dada um desses casos separadamente.

Caso I

Para uma integral que envolva um radical do tipo $\displaystyle \sqrt{a^2-x^2}$, fazemos a mudança de variável de $x$ para $\theta$. A substituição deve ser apropriada e fica melhor observada no triângulo retângulo:

Temos que:
$$\begin{equation*} \text{sen}(\theta) = \frac{x}{a}\\ \ \\ x = a \ \text{sen}(\theta) \end{equation*}$$

Assim, $x = a\ \text{sen}(\theta)$ substitui $\displaystyle \sqrt{a^2-x^2}$ por $a\ \cos(\theta)$, pois:

$$\begin{equation*} a^2 - x^2 = a^2 - \left(a\ \text{sen}(\theta)\right)^2\\ \ \\ a^2 - x^2 = a^2 - a^2\  \text{sen}^2(\theta)\\ \ \\ a^2 - x^2 = a^2 \left(1-\text{sen}^2(\theta)\right) \end{equation*}$$

E pela identidade trigonométrica dada em $(1)$, obtemos:

$$\begin{equation*} a^2 - x^2 = a^2\ \cos^2(\theta) \end{equation*}$$

Extraindo a raiz de ambos os membros da equação, obtemos:

$$\begin{equation*} \sqrt{a^2-x^2} = a\ \cos(\theta) \end{equation*}$$
Justificando a substituição.

Caso II

Para uma integral que envolva um radical do tipo $\displaystyle \sqrt{a^2+x^2}$, fazemos a mudança de variável de $x$ para $\theta$. Observando o triângulo retângulo:

Temos que:
$$\begin{equation*} \text{tg}(\theta) = \frac{x}{a}\\ \ \\ x = a\ \text{tg}(\theta) \end{equation*}$$

Assim, $x = a\ \text{tg}(\theta)$ substitui $\displaystyle \sqrt{a^2 +x^2}$ por $a\ \text{sec}(\theta)$, pois:

$$\begin{equation*} a^2 + x^2 = a^2 + \left(a\ \text{tg}(\theta)\right)^2\\ \ \\ a^2 + x^2 = a^2 + a^2\ \text{tg}^2(\theta)\\ \ \\ a^2 + x^2 = a^2 \left( 1 + \text{tg}(\theta) \right) \end{equation*}$$

E pela identidade trigonométrica da em $(2)$, obtemos:

$$\begin{equation*} a^2 + x^2 = a^2\ \text{sec}^2(\theta) \end{equation*}$$

Extraindo a raiz de ambos os membros da equação acima, obtemos:

$$\begin{equation*} \sqrt{a^2+x^2} = a\ \text{sec}(\theta) \end{equation*}$$
Justificando a substituição.

Caso III

Para uma integral que envolva um radical do tipo $\displaystyle \sqrt{x^2-a^2}$, fazemos a mudança de variável de $x$ para $\theta$. Observando o triângulo retângulo:

Temos que:
$$\begin{equation*} \text{sec}(\theta) = \frac{x}{a}\\ \ \\ x = a\ \text{sec}(\theta) \end{equation*}$$

Assim, $x=a\ \text{sec}(\theta)$ substitui $\displaystyle \sqrt{x^2-a^2}$ por $a\ \text{tg}(\theta)$, pois:

$$\begin{equation*} x^2 - a^2 = \left(a\ \text{sec}(\theta)\right)^2 - a^2\\ \ \\ x^2 - a^2 = a^2 \text{sec}^2(\theta) - a^2\\ \ \\ x^2 - a^2 = a^2 \left(\text{sec}^2(\theta)-1\right) \end{equation*}$$

E pela identidade trigonométrica dada em $(3)$, obtemos:

$$\begin{equation*} x^2-a^2 = a^2 \ \text{tg}^2(\theta) \end{equation*}$$

Extraindo a raiz de ambos os membros da equação, obtemos:

$$\begin{equation*} \sqrt{x^2-a^2} = a\ \text{tg}(\theta) \end{equation*}$$
Justificando a substituição.

Com base nos resultados obtidos acima, podemos montar uma tabela:

Vejam que, para representar graficamente as substituições sugeridas no triângulo retângulo, o radical ficará sempre no lado do triângulo que não é utilizado pela relação trigonométrica:

• Caso I: Usa-se $x = a\ \text{sen}(\theta)$; logo, o radical aparece no cateto adjacente a $\theta$;
• Caso II: Usa-se $a\ \text{tg}(\theta)$ ; logo, o radical aparece na hipotenusa;
• Caso III: Usa-se $a\ \text{sec}(\theta)$; logo, o radical aparece no cateto oposto a $\theta$.

Exemplo 1:

Calcular a integral $\displaystyle \int \frac{\sqrt{a^2-x^2}}{x}\ dx$.

Essa é uma integral do tipo I. Vamos fazer a representação no triângulo retângulo:

Assim, escrevemos:
$$\begin{gather*} \text{sen}(\theta) = \frac{x}{a}\\ \ \\ x = a\ \text{sen}(\theta) \tag{a}\\ \ \\ dx = a\ \cos(\theta)\ d\theta \tag{b}\\ \ \\ \sqrt{a^2 - x^2} = a\ \cos(\theta)\tag{c} \end{gather*}$$
Assim, seja a integral:
$$\begin{equation*} I = \int \frac{\sqrt{a^2-x^2}}{x}\ dx\\ \ \\ I = \int \frac{a\ \cos(\theta)}{a\ \text{sen}(\theta)}\ a\ \cos(\theta)\ d\theta\\ \ \\ I = a \int \frac{\cos^2(\theta)}{\text{sen}(\theta)}\ d\theta\\ \ \\ I = \ \int \frac{1 - \text{sen}^2(\theta)}{\text{sen}(\theta)}\ d\theta\\ \ \\ I = a \int \left( \frac{1}{\text{sen}(\theta)}-\text{sen}(\theta) \right)\ d\theta\\ \ \\ I =  a \int \left( \text{cosec}(\theta) - \text{sen}(\theta)\right)\ d\theta\\ \ \\ I = -a\ \ln \left( \text{cosec}(\theta) + \text{cotg}(\theta)\right) + a\ \cos(\theta) + C \end{equation*}$$

Devemos agora reescrever o resultado em termos da variável original $x$. Observando o triângulo retângulo, devemos encontrar as relações trigonométricas que aparecem no resultado acima. assim:

$$\begin{equation*} \text{cosec}(\theta) = \frac{a}{x}\\ \ \\ \text{cotg}(\theta) = \frac{\sqrt{a^2-x^2}}{x}\\ \ \\ \cos(\theta) = \frac{\sqrt{a^2-x^2}}{a} \end{equation*}$$
Assim:
$$\begin{equation*} I = -a \ln \left( \frac{a}{x} + \frac{\sqrt{a^2-x^2}}{x}\right)  + a\ \frac{\sqrt{a^2-x^2}}{a} + C\\ \ \\ I =\sqrt{a^2-x^2} - a \ \ln \left( \frac{a+\sqrt{a^2-x^2}}{x} \right) + C\\ \ \\ I = \sqrt{a^2 - x^2} - \ln \left(a + \sqrt{a^2-x^2} \right) + a\ \ln (x) + C \end{equation*}$$

Exemplo 2:

Calcular a integral $\displaystyle \int \frac{dx}{\sqrt{a^2+x^2}}$.

Esta é uma integral do tipo II. Vamos fazer a representação no triângulo retângulo:

Assim, escrevemos:
$$\begin{gather*} \text{tg}(\theta) = \frac{x}{a}\\ \ \\ x = a\ \text{tg}(\theta) \tag{a}\\ \ \\ dx = a\ \text{sec}^2(\theta)\ d\theta \tag{b}\\ \ \\ \sqrt{a^2+x^2} = a\ \text{sec}(\theta) \tag{c} \end{gather*}$$
Assim, seja a integral:
$$\begin{equation*} I = \int \frac{dx}{\sqrt{a^2+x^2}}\\ \ \\ I = \int \frac{a\ \text{sec}^2(\theta)}{a\ \text{sec}(\theta)}\ d\theta \\ \ \\ I = \int \text{sec}(\theta)\ d\theta\\ \ \\ I = \ln \left( \text{sec}(\theta) + \text{tg}(\theta) \right)  + C \end{equation*}$$

Vamos agora reescrever o resultado em termos da variável original $x$. Observando o triângulo retângulo, encontramos as relações:

$$\begin{equation*} \text{sec}(\theta) = \frac{\sqrt{a^2+x^2}}{a}\\ \ \\ \text{tg}(\theta) = \frac{x}{a} \end{equation*}$$
Assim:
$$\begin{equation*} I = \ln \left( \frac{\sqrt{a^2+x^2}}{a}+\frac{x}{a} \right) + C\\ \ \\ I = \ln \left(\frac{\sqrt{a^2+x^2}+x}{a} \right) + C\\ \ \\ I = \ln \left(\sqrt{a^2+x^2}+x\right) - \ln(a) + C \end{equation*}$$

Como $C$ é uma constante arbitrária e $\ln(a)$ também é uma constante, podemos reescrever o resultado como:

$$\begin{equation*} I = \ln \left( \sqrt{a^2+x^2}+x \right)+ C \end{equation*}$$

Exemplo 3:

Calcular a integral $\displaystyle \int \frac{\sqrt{x^2-a^2}}{x}\ dx$.

Esta é uma integral do tipo III. Vamos fazer a representação no triângulo retângulo:

Assim escrevemos:
$$\begin{gather*} \text{sec}(\theta) = \frac{x}{a}\\ \\\ x = a\ \text{sec}(\theta) \tag{a}\\ \ \\ dx = a\ \text{sec}(\theta)\ \text{tg}(\theta)\ d\theta \tag{b} \\ \ \\ \sqrt{x^2-a^2} = a\ \text{tg}(\theta) \tag{c} \end{gather*}$$
Assim, seja a integral:
$$\begin{equation*} I = \int \frac{\sqrt{x^2-a^2}}{x}\ dx\\ \ \\ I = \int \frac{a\ \text{tg}(\theta)}{a\ \text{sec}(\theta)}\ a \ \text{sec}(\theta)\ \text{tg}(\theta)\ d\theta\\ \ \\ I = \int a\ \text{tg}^2(\theta)\ d\theta\\ \ \\ I = a \int \left(\text{sec}^2(\theta)-1\right)\ d\theta\\ \ \\ I = a\ \text{tg}(\theta) - a\ (\theta) + C \end{equation*}$$

Vamos reescrever o resultado em termos da variável original $x$. Observando o triângulo encontramos as relações:

$$\begin{equation*} \text{tg}(\theta) = \frac{\sqrt{x^2-a^2}}{a}\\ \ \\ \theta = \text{arctg}\left( \frac{\sqrt{x^2-a^2}}{a} \right) \end{equation*}$$
Assim:
$$\begin{equation*} I = a\ \frac{\sqrt{x^2-a^2}}{a} - a\ \text{arctg}\left( \frac{\sqrt{x^2-a^2}}{a} \right)+C\\ \ \\ I = \sqrt{x^2-a^2} - a\ \text{arctg} \left( \frac{\sqrt{x^2-a^2}}{a} \right) + C \end{equation*}$$

Exemplo 4:

Calcular a integral $\displaystyle \int \frac{dx}{x^2\sqrt{16-x^2}}$.

Esta é uma integral do tipo I. Vamos fazer a representação no triângulo retângulo:

Assim, escrevemos:
$$\begin{gather*} \text{sen}(\theta) = \frac{x}{4}\\ \ \\ x = 4\ \text{sen}(\theta) \tag{a}\\ \ \\ dx = 4\ \cos(\theta)\ d\theta \tag{b}\\ \ \\ \sqrt{16-x^2} = 4\ \cos(\theta) \tag{c} \end{gather*}$$
Seja a integral:
$$\begin{equation*} I = \frac{dx}{x^2 \sqrt{16-x^2}}\\ \ \\ I = \frac{4\ \cos(\theta)\ d\theta}{\left(4\ \text{sen}(\theta)\right)^2\ 4\ \cos(\theta)}\\ \ \\ I = \frac{1}{16} \int \frac{d\theta}{\text{sen}^2(\theta)}\\ \ \\ I = \frac{1}{16} \int \text{cosec}^2(\theta)\ d\theta\\ \ \\ I = -\frac{1}{16} \text{cotg}(\theta)\ d\theta +C \end{equation*}$$

Agora, reescrevemos o resultado em termos da variável original $x$. Observando o triângulo retângulo, encontramos a relação:

$$\begin{equation*} \text{cotg}(\theta) = \frac{\sqrt{16-x^2}}{x} \end{equation*}$$
Assim:
$$\begin{equation*} I = -\frac{\sqrt{16-x^2}}{16x} + C \end{equation*}$$

Exemplo 5:

Calcular a integral $\displaystyle \int \frac{dx}{x^2 \sqrt{4+x^2}}$.

Esta é uma integral do tipo II. Vamos fazer a representação no triângulo retângulo:

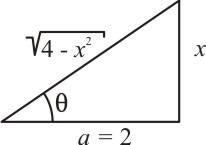
Assim, escrevemos:
$$\begin{gather*} \text{tg}(\theta) = \frac{x}{2}\\ \ \\ x = 2\ \text{tg}(\theta) \tag{a}\\ \ \\ dx = 2\ \text{sec}^2(\theta)\ d\theta \tag{b}\\ \ \\ \sqrt{4+x^2} = 2\ \text{sec}(\theta) \tag{c} \end{gather*}$$
Seja a integral:
$$\begin{equation*} I = \int \frac{dx}{x^2 \sqrt{4+x^2}}\\ \ \\ I = \int \frac{2\ \text{sec}^2(\theta)\ d\theta}{\left(2\ \text{tg}(\theta)\right)^2\ 2\ \text{sec}(\theta)}\\ \ \\ I = \frac{1}{4} \int \frac{\text{sec}(\theta)}{\text{tg}^2(\theta)}\ d\theta\\ \ \\ I = \frac{1}{4} \int \text{cosec}^2(\theta)\ \cos(\theta)\ d\theta\\ \ \\ I = \frac{1}{4} \text{cosec}(\theta)+C \end{equation*}$$

Reescrevendo o resultado em termos da variável original $x$ e utilizando as relações observadas no triângulo retângulo, fazemos:

$$\begin{equation*} \text{cosec}(\theta) = \frac{4+x^2}{x} \end{equation*}$$
Assim:
$$\begin{equation*} I = \frac{1}{4} \cdot \frac{\sqrt{4+x^2}}{x}+C\\ \ \\ I = \frac{\sqrt{4+x^2}}{4x}+C \end{equation*}$$

Exemplo 6:

Calcular a integral $\displaystyle \int \frac{dx}{x^3 \sqrt{x^2-25}}$.

Esta é uma integral do tipo III. Vamos fazer a representação no triângulo retângulo:

Assim, escrevemos:
$$\begin{gather*} \text{sec}(\theta) = \frac{x}{5}\\ \ \\ x = 5\ \text{sec}(\theta) \tag{a}\\ \ \\ dx = 5\ \text{sec}(\theta)\ \text{tg}(\theta)\ d\theta \tag{b}\\ \ \\ \sqrt{x^2-25} = 5\ \text{tg}(\theta) \tag{c} \end{gather*}$$
Seja a integral:
$$\begin{equation*} I = \int \frac{dx}{x^3 \sqrt{x^2-25}}\\ \ \\ I = \int \frac{5\ \text{sec}(\theta)\ \text{tg}(\theta)\ d\theta}{(5\ \text{sec}(\theta))^3 \ 5\ \text{tg}(\theta)}\\ \ \\ I = \int \frac{5\ \text{sec}(\theta)\ \text{tg}(\theta)\ d\theta}{125\ \text{sec}^3(\theta)\ 5\ \text{tg}(\theta)}\\ \ \\ I = \frac{1}{125} \int \frac{d\theta}{\text{sec}^2(\theta)}\\ \ \\ I = \frac{1}{125} \int \cos^2(\theta)\ d\theta\\ \end{equation*}$$

A integral de $\cos^2(\theta)$ é $\displaystyle \frac{1}{2}(\theta + \text{sen}(\theta)\ \cos(\theta))$, assim:

$$\begin{equation*} I = \frac{1}{125} \cdot \frac{1}{2}(\theta + \text{sen}(\theta)\ \cos(\theta))+C\\ \ \\ I = \frac{1}{250} (\theta + \text{sen}(\theta)\ \cos(\theta))+C \end{equation*}$$

Agora, representamos o resultado em termos da variável original $x$. Observando o triângulo retângulo, encontramos as relações:

$$\begin{equation*} \text{sen}(\theta) = \frac{\sqrt{x^2-25}}{x}\\ \ \\ \cos(\theta) = \frac{5}{x}\\ \ \\ \theta = \text{arctg} \left( \frac{5}{\sqrt{x^2-25}} \right) \end{equation*}$$
Assim:
$$\begin{equation*} I = \frac{1}{250} \left( \text{arctg}\left( \frac{5}{\sqrt{x^2-25}} \right) + \frac{\sqrt{x^2-25}}{x}\cdot \frac{5}{x} \right) + C\\ \ \\ I = \frac{1}{250} \left( \frac{5\sqrt{x^2-25}}{x^2} + \text{arctg} \left( \frac{5}{\sqrt{x^2-25}} \right) \right) + C \end{equation*}$$

Exemplo 7:

Para ilustrar o uso desse método, vamos determinar a equação da tractriz, que é uma curva definida pela trajetória de um objeto arrastado ao longo de um plano horizontal por um fio de comprimento constante quando a outra extremidade do fio se move ao longo de uma reta no plano. A palavra tractriz provém do latim tractum, que significa "draga". Vamos considerar um plano formado por eixos ortogonais $x\ y$ e o objeto comece no ponto $(a,\ 0)$ com a outra extremidade do fio na origem. Se esta se move para cima ao longo do eixo dos $y$:

o fio será sempre tangente à curva e o comprimento da tangente entre o eixo dos $y$ e o ponto de contato será sempre igual a $a$. O coeficiente angular da tangente é dado pela fórmula:

$$\begin{equation*} \frac{dy}{dx} = -\frac{\sqrt{a^2-x^2}}{x} \end{equation*}$$

Separando as variáveis e usando o resultado do exemplo 1, temos:

$$\begin{equation*} y = - \int \frac{\sqrt{a^2-x^2}}{x}\ dx \\ \ \\ y = a\ \ln \left( \frac{a+\sqrt{a^2-x^2}}{x} \right) - \sqrt{a^2-x^2}+C \end{equation*}$$
Quando $x=a$, $y=0$ e $C=0$. Logo:
$$\begin{equation*} y = a\ \ln \left( \frac{a+\sqrt{a^2-x^2}}{x} \right)-\sqrt{a^2-x^2} \end{equation*}$$
que é a equação da tractriz.

Se as extremidades do fio movem-se para baixo no eixo dos $y$, então uma outra parte da curva é gerada. Se girarmos essas duas partes em torno do eixo dos $y$, a superfície resultante será uma pseudo-esfera, com forma de uma "trombeta dupla".

Tente resolver estes exercícios:

$$\begin{equation*} 1) \qquad \int \frac{x^3}{\sqrt{9-x^2}}\ dx \\ \ \\ 2) \qquad \int \frac{x^2}{(4-x^2)^{3/2}}\ dx\\ \ \\ 3) \qquad \int \frac{dx}{x^2\ \sqrt{x^2-9}}\\ \ \\ 4) \qquad \int \frac{dx}{x^3\ \sqrt{x^2-4}}\\ \ \\ 5) \qquad \int \sqrt{9-4x^2}\ dx \end{equation*}$$

Links para este artigo:

• http://bit.ly/Subst-Trig
• https://www.obaricentrodamente.com/2012/06/integracao-por-substituicao.html

Referências:

• Cálculo com Geometria Analítica V1 - Simmons
• Cálculo V1 - Munen & Foulis
• Cálculo Diferencial e Integral - Frank Ayres Jr

Veja mais:

• Integração por Frações Parciais – Fatores Lineares 
• Integração por Frações Parciais – Fatores Quadráticos Irredutíveis 
• Método de Integração por Substituição 
• Método de Integração por Partes