Wilhelm Otto Ludwing Specht (1907-1985) foi um matemático alemão que desenvolveu uma construção geométrica que aproxima a retificação da circunferência com uma precisão de 5 casas decimais.
Construção:
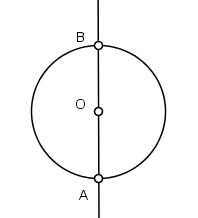
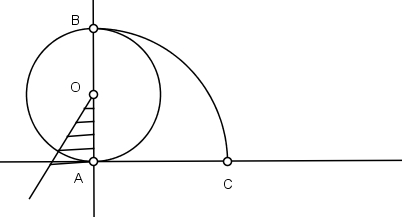
1) Descreva uma circunferência de raio R e de centro O.
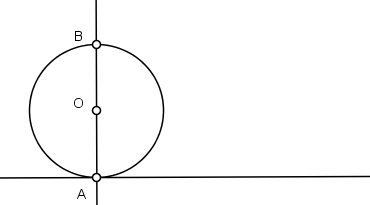
2) Trace o diâmetro vertical AB prolongando na direção de B.
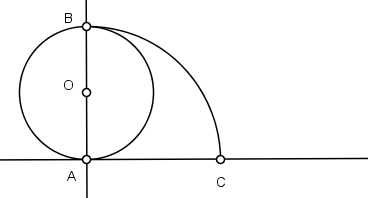
3) Trace uma perpendicular por B.
4) Descreva um arco de raio AB e marque o ponto C na intersecção com a perpendicular.
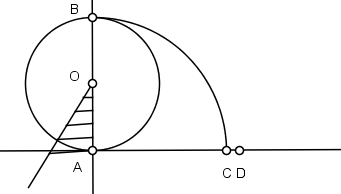
5) Divida o raio AO em cinco partes iguais.
6) Com centro em C, descreva um arco de raio igual a 1/5 do raio AO e marque o ponto D na perpendicular.
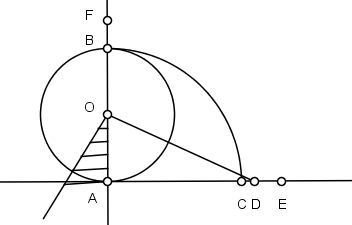
7) Com centro em D, descreva um arco de raio igual a 2/5 do raio AO e marque o ponto E na perpendicular.
8) Com centro em A e raio OD, marque o ponto F no prolongamento do diâmetro AB.
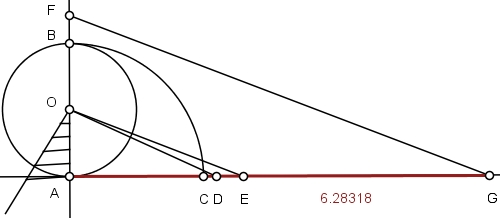
9) Una os pontos OE e trace uma paralela a OE que passe por F, marcando o ponto G na intersecção com a perpendicular.
10) O segmento AG é a aproximação da circunferência retificada.
Demonstração:
De acordo com a construção, o segmento AG aproxima a circunferência. Para sua determinação, podemos utilizar semelhança de triângulos, onde:
Assim, temos a relação:
A medida AE é dada por:
A medida AF = OD e a medida OD é dada por:
Aplicando os valores encontrados em (2) e (3) na relação (1), obtemos:
Que podemos escrever como:
Se o raio da circunferência é unitário, então o segmento AG aproxima a circunferência com cinco casas decimais corretas:
Que nos remete a uma aproximação de π a:
Uma aproximação muito boa.
Veja mais:
Retificação da Circunferência Parte 1, Parte 2, Parte 3, Parte 4, Parte 5
Divisão de um Seguimentos em Partes Iguais
Aproximação de π Como Soma de Dois Números Irracionais




![clip_image002[24] clip_image002[24]](http://lh4.ggpht.com/-Co_2o0rCQlk/UPGM28UD3pI/AAAAAAAAXw8/EDiUvgXbD-o/clip_image002%25255B24%25255D_thumb.gif?imgmax=800)

Olá, Kleber!!!!
ResponderExcluirQuer dizer que aí... a medida de "ouro", a medida real... não será encontrada!!!! Mas, eu fico mesmo agradecido por você ter ensinado tão bem, como devemos atingir, pelo menos, a medida de "prata"!!!! KKKKKKKKKKKKK!!!!!!!!!! Garanto que não está entendendo nada, não é???? Rsrsrsrs!!!! É brincadeira!!!! É porque... Ag é o símbolo químico da prata e, o segmento AG obtido ali naquela construção me fez lembrar o precioso metal!!!!
Parabéns, pela excelente postagem, parceiro e, eu fico imaginando... quanto o Wilhelm Otto Ludwing Specht, deve ter queimado de fosfato no cérebr,o para conseguir chegar a essa interessante e elegante construção geométrica!!!!
Um abraço!!!!!
Olá Educador Kleber, Felicidades!
ResponderExcluirEstou aqui para convidar você a conhecer o Projeto Educadores Multiplicadores. O objetivo é unir e divulgar blog de educadores.
DIVULGUE SEU BLOG no EDUCADORES MULTIPLICADORES e fique em evidência. Compartilhe saberes!
A blogosfera é carente de blogs que tenham informações relevantes, mas você está contribuindo para que ela se torne cada vez mais rica em conhecimentos.
Esta parceria é exclusiva para blogs de Educadores e Professores que escrevem conteúdos ligados diretamente à Educação.
Faça parte da família dos Multiplicadores! Seu blog ficará mais conhecido entre os professores/educadores, alunos e escolas de todo o Brasil e Portugal. Amplie seu público!
Permita-me deixar o link para o blog Marquecomx (Divulgaremos seu blog também nas redes sociais): MARQUECOMX.
Abraços, fiquemos na Paz de Deus e até breve.
Irivan Rodrigues
Olá querido seja bem vindo aos multiplicadores, excelente conteúdo no seu blog, já estou seguindo .Aguardo sua visita http://proaiseartedeeducar.blogspot.com.br
ResponderExcluirUma ótima semana!
Boa tarde Kleber!!!
ResponderExcluirRealmente você ama Matemática.
Tenho plena em matemática, mas fiz pós em educação infantil e optei por trabalhar apenas com os pequenos.
Se me fizer perguntas difíceis sobre matemática, vou ter que pesquisar para lhe responder. (risos) Já tenho uns dez anos de formada. #fato.
Seja sempre bem vindo no meu cantinho.
Espero nos vermos mais vezes...
Vim através do blog: Educadores Multiplicadores.
Abraços da Bia!!!
Olá Kleber!Sou dos Educadores Multiplicadores.
ResponderExcluirSeja bem vindo!
Que paixão você tem pela matemática.Parabéns.
Um abraço.
Valdete Cantú
Olá, cheguei aqui através dos Educadores Multiplicadores.
ResponderExcluirParabéns pelo blog. Admiro muito os professores de Matemática, pois acho um grande desafio.
Professora Genis
http://www.reciclandocomamamae.com/
http://redeeducacaoemfoco.blogspot.com.br/
Bom dia Kleber!!!
ResponderExcluirObrigada por seguir meu blog. Seja sempre muito bem vindo. Espero nos vermos mais vezes...
Tenha uma semana feliz e abençoada.
Abraços...da Bia!!!